Contents
In the realm of algebraic expressions, the (a+b)^3 formula stands as a fundamental and often perplexing concept. As we delve into the depths of this formula, we’ll unravel its secrets, exploring its significance, applications, and the underlying mathematics. Whether you’re a student seeking clarity or a curious mind eager to understand, this article will break down the (a+b)^3 formula in a way that’s both accessible and engaging.
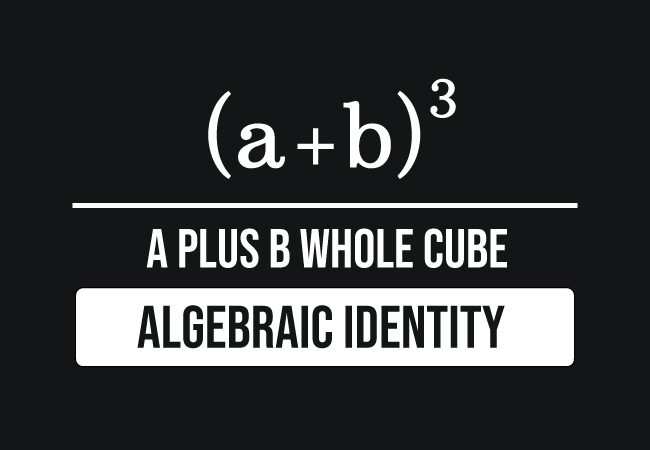
What is the (a+b)^3 Formula?
The (a+b)^3 formula is a vital expression in algebra, representing the cube of a binomial. It can be expressed as:
(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
To comprehend this formula better, let’s break it down step by step.
Step 1: a^3
The first term, a^3, represents the cube of the ‘a’ value. In simpler terms, it means multiplying ‘a’ by itself three times.
Step 2: 3a^2b
The second term, 3a^2b, involves three components. It starts with ‘3,’ signifying the number of combinations to get from ‘a’ cubed to ‘b’ cubed. Then, we have ‘a^2,’ indicating that ‘a’ is squared. Finally, ‘b’ is left unaltered.
Step 3: 3ab^2
Similarly, the third term, 3ab^2, follows the same logic as the second term. We again have ‘3’ for the combinations, ‘a’ remains unaltered, and ‘b’ is squared this time.
Step 4: b^3
The final term, b^3, represents the cube of the ‘b’ value, signifying that ‘b’ is multiplied by itself three times.
Applications of the (a+b)^3 Formula
Now that we understand the components of the (a+b)^3 formula, let’s explore its real-world applications.
1. Binomial Expansion
One of the primary applications of this formula is binomial expansion. It allows us to expand expressions like (a+b)^3 into a series of terms, making it easier to work with.
2. Probability Calculations
In probability theory, this formula plays a crucial role in solving problems involving combinations and permutations. It helps calculate the probability of specific outcomes in various scenarios.
3. Engineering and Physics
Engineers and physicists often use the (a+b)^3 formula when dealing with complex equations, especially in fields such as fluid dynamics and electromagnetism.
Also Read :
Understanding the Math Behind It
To fully grasp the (a+b)^3 formula, it’s essential to understand the mathematical reasoning behind it. This formula is derived using the binomial theorem, a powerful tool in combinatorics and algebra.
Conclusion
In conclusion, the (a+b)^3 formula may appear intimidating at first glance, but breaking it down into its components and exploring its applications can make it more accessible. It serves as a fundamental concept in algebra, with practical implications in various fields. Embracing the intricacies of this formula can unlock a deeper understanding of algebraic expressions.